Infraschall ist wie jeder Schall zunächst einfach bewegte Luft. Die Besonderheit des Infraschalls ist, dass er unterhalb des Hörvermögens des Menschen liegt. Die obere Grenze vom Infraschall liegt bei 16 bis 20 Hz. Im Gegensatz dazu ist der Ultraschall oberhalb unseres Hörvermögens ab 20kHz.
Infraschall ist allgegenwärtig. Es gibt viele natürliche Quellen dafür:
Aber auch wir Menschen erzeugen Infraschall
Infraschall kann durch Mikrofone, Mikrobarometer, Drucksensoren gemessen werden. Die Mikrobarometer gehören zu den empfindlichsten Geräten und werden im professionellen Bereich eingesetzt. Sie dienen zum Beispiel der weltweiten Überwachung von möglichen Atomexplosionen.
Infraschall hat zunächst keine speziellen physikalischen Eigenschaften. Die Besonderheit zieht sich nur auf die geringe Frequenz und auf unsere Wahrnehmung.
Grundsätzlich gilt: je tiefer die Frequenz des Schalls, desto größer ist die Reichweite in der Atmosphäre. Die Druckwelle der Zar-Wasserstoffbombe umrundete mehrfach die Erde.
Infraschall hat aufgrund seiner Ausbreitungsfähigkeit über große Entfernungen potenzielle militärische Anwendungen. Allerdings sind die ethischen Implikationen und internationalen Vorschriften im Zusammenhang mit einer solchen Verwendung erheblich.
Ja, Infraschall ist bei ausreichend hohem Pegel sogar tödlich. Denken Sie an die Druckwelle einer Explosion. Obwohl Infraschall für Menschen im Allgemeinen nicht hörbar ist, kann er bei ausreichend hoher Intensität dennoch physiologische Auswirkungen haben. Zu diesen Auswirkungen können Übelkeit, Schwindel und Unwohlsein gehören.
Durch den Ausbau der Windräder ist Infraschall ein häufiges Thema.
Sie benötigen hierfür spezielle Messgeräte. Normale Schallpegelmesser sind hierfür ungeeignet, da diese meist nur ab 20Hz messen können. Mit speziellen Messgeräten können auch Frequenzen unterhalb 1 Hz verlässlich gemessen werden. Gerade bei Windrädern muss man die Windgeschwindigkeit beachten.
Wie bieten geeignete Messgeräte an, führen selbst Messungen vor Ort durch oder vermieten auch Ausrüstung an Sachkundige.
Infraschall ist Teil unserer natürlichen Umgebung. Es gibt bisher keine Hinweise, dass Infraschall, der in der Größenordnung der natürlichen Hintergrund-Pegels liegt, zu irgendwelchen Schäden führt. Infraschall entsteht durch banale Dinge im Alltag. Das Öffnen eines Kühlschranks erzeugt um Größenordnungen mehr Infraschall als ein Windrad in 300m Entfernung.
Eine Funkstrecke für ein Messmikrofon ist eine verlockende Alternative zu einem kabelgebundenen Messsystem. Leider sind auf dem Markt nur wenige Lösungen verfügbar. Das Problem ist weniger die technische Lösung. Durch den Gesetzgeber sind die mögliche Sendeleistung und der Funk-Frequenzbereich stark begrenzt. Die verfügbaren Frequenzen müssen mit verschieden Diensten und Geräten geteilt werden. Dadurch sind Reichweite, Signal-Bandbreite und Störunempfindlichkeit deutlich eingeschränkt.
Es gibt im Bereich der Studio-Technik jedoch eine große Vielzahl von Funk-Systemen. Diese Funkmodule sind primär dafür gedacht, zwischen Mikrofon und Mischpult geschaltet zu werden. Solche Funkstrecken lassen sich zunächst in zwei Kategorien aufteilen:
rein analoge Funkstrecken, die typischerweise FM (Frequenz-Modulation) verwenden.
digitale Systeme. Hier wird das analoge Mikrofon-Signal zunächst digitalisiert und als digitales Signal über die Funkstrecke übertragen. Im Empfänger wird daraus wieder ein analoges Signal erzeugt.
Die Funkstrecken verwenden eine Vielzahl von Frequenzbändern. Diese sind vielfach international/EU bzw. national standardisiert. Weit verbreitet ist das 2,4 GHz Band für digitale Funkstrecken, das aber häufig durch WLAN Geräte, Bluetooth usw. bereits belegt ist. Die große Einschränkung bei Funkstrecken egal ob analog oder digital ist die verfügbare Bandbreite, dies ist weniger technisch bedingt, sondern dadurch, dass nur schmale Frequenzbereiche für Funkstrecken zugelassen sind. Daher ist die Bandbreite die wertvollste Ressource. Daher verwenden die Funkstrecken verschiedene Techniken, um Bandbreite zu sparen. Das sind zum Beispiel analoge Kompressionstechniken, aber auch sehr fortgeschrittene digitale Verfahren, die ähnlich dem MP3 Standard funktionieren.
Ein hochwertiges Messmikrofon hat einen Dynamikbereich von 15dB bis 140dB, also ein Bereich von 125dB. Dieser hohe Dynamikbereich übersteigt zum Beispiel die Dynamik eines klassischen CD-Spielers und noch viel mehr die Dynamik einer Funkstrecke. Diese ist gar nicht in der Lage ist die Dynamik eines CD-Spielers von circa 96dB unkomprimiert übertragen zu können. Funkstrecken verringern daher die Bandbreite des analogen Signals und sie begrenzen auch die Dynamik. Viele Systeme haben eine AGC (Automatic Gain Control) eingebaut. Alle diese Techniken zur Kompression sind für Messtechnik ungeeignet und verfälschen das Messergebnis
Für eine Funk-gebundene Messstrecke benötigen Sie:
Moderne Messmikrofone in der klassischen Bauform als Kondensatormikrofon verändern ihre Paramter selbst über Jahre nur sehr wenig. Bei sorgfältiger Lagerung sind sie prInzipiell über Jahrzehnte verwendbar. Allerdings sind Messmikrofone im rauhen Alltag anderen Belastungen ausgesetzt.
Wie oft kommt es vor, dass ein Messmikrofon einfach vom Tisch fällt?
Von aussen ist vielleicht nur eine kleine Beule am Schutzgitter erkennbar. Aber......
Erste Hinweise liefert eine Sichtprüfung der Membran. Diese muss glatt anliegen und darf keine Beulen, Dellen oder Löcher haben. Dies wäre ein Totalschaden.
Das folgende Bild zeigt drei 1/2" Kapseln ohne Schutzgitter.
Die linke Kapsel ist normal funktionsfähig mit glatter Membran.
Bei der mittleren wurde die Membran entfernt und man erkennt die Gegenelektrode. Die Löcher in der Gegenlektrode dienen einer gezielten Dämpfung der Membranbewegung.
Die rechte Kapsel ist durch Fallen beschädigt. Die Membran liegt nicht mehr glatt an. In diesem Beispiel ist der Defekt deutlich sichtbar. In der Praxis können die Schäden jedoch subtiler sein und optisch kaum erkennbar sein.

Auch wenn zunächst keine Schäden direkt sichtbar sind, kann die Membran eventuell nicht mehr, die vom Hersteller präzise eingestellte, mechanische Spannung besitzen.
Letzlich muss bei unklaren Kapseln der Frequenzgang vermessen im Labor vermessen werden. Nur so kann die einwandfreie Einhaltung der Spezifikation durch den Hersteller geprüft werden.
Wir führen solche Messungen wirtschaftlich mit einer Präzisionsdruckkammer durch. Wir verwenden dafür einen automatisierten Messplatz, der alle relevanten Parameter erfasst. Sie erhalten einen übersichtlichen Bericht.
Wie können Sie die korrekte Funktion Ihres Schallplattenspielers überprüfen?
Es gibt eine Vielzahl von Testschallplatten auf dem Markt, dies sind teilweise sehr hochwertige z.B. von Bruel&Kjaer. Die meisten sind jedoch historisch und nur noch gebraucht verfügbar. Der wirkliche Zustand ist damit unklar.
Die Testschallplatte von Clearaudio ist eine Neuproduktion und zeigt daher ein definiertes Verhalten. Daher haben wir uns mit unserer Auswertung auf diese LP spezialisiert.
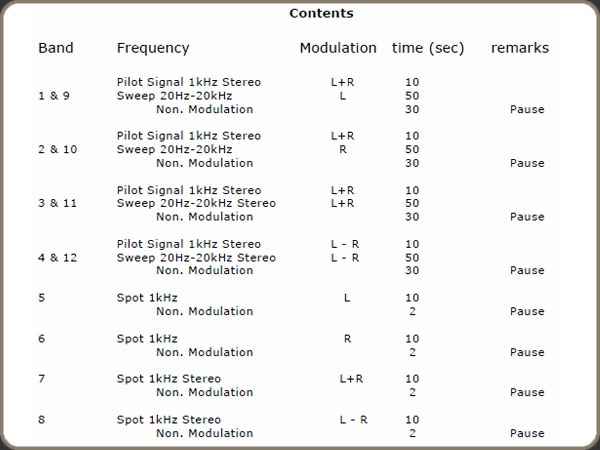
Diese LP enthält u.a. eine Aufnahme mit einem Pilotton von 1kHz und ein Sweep von 20-20kHz.
Frequenzgang des gesamten Systems vom Tonabnehmer bis zum Ausgang Ihres Phono-Verstärkers.
Drehzahl
Gleichlaufschwankungen (Wow&Flutter)
Übersprechen
Verzerrungen über der Frequenz
Die Spur beginnt mit einem Pilotton mit der Frequenz von 1kHz und einer Länge von 10s. Mit diesem Pilotton können bereits Frequenzabweichungen ermittelt werden und die Pegel kalibriert werden. Danach folgt eine kurze Pause. Dananch folgt der "Sweep", ein Gleitton von 20-20kHz innerhalb von 50s. Dieser Sweep wird in verschiedenen Aufnahmen auf die beiden Kanäle verteilt. Es gibt Aufnahmen nur mit jeweils einem Kanal, sowie der Summe und der Differenz auf beiden Kanälen. Auf diese Weise kann das Übersprechen ermittelt werden.
Schauen wir uns zunächst den Verlauf des Pegels in dB über der Zeit an.
_RMS_vs_time.png)
Man erkennt deutlich, den relativ konstanten Pilotton, die Pause und den Sweep.
Interssanter wird es, wenn man die Momentanfrequenz misst und auch wieder über der Zeit darstellt.
_freq_vs_time.png)
Bitte beachten Sie, dass die Y-Achse (Frequenzachse) logarithmisch ist. In dieser Darstellung ist der Sweep linear. Das wiederum bedeutet, dass die Frequenz innerhalb des Sweeps - wie es in der Audiotechnik üblich ist - exponentiell erhöht wird.
Schauen wir uns zunächst den Pilotton genauer an. In der Übersicht erscheint er zwar konstant mit 1000Hz, aber....
_pilot_freq_vs_time.png)
Man erkennt eine Abweichung von ca. 0.6% (994Hz statt 1000Hz) und eine Schwankung, die auch als Wow&Flutter bezeichnet wird. Weiter unten in diesem Artikel werten wir die Drehzahlabweichungen und Gleichlaufschwankungen genauer aus.
Aus dem Sweep kann der Pegel über der Momentanfrequenz aufgetragen werden. Dies ist der klassische Frequenzgang.
Sie können damit den Tonabnehmer und die RIAA-Entzerrung prüfen.
_freq_response.png)
Das Spektrogram ist ein hilfreiches Werkzeug, um den Pegel über der Zeit UND der Frequenz darzustellen.
_spectrogram.png)
Man erkennt den Signalverlauf in einem Überblick.
Im folgenden Bild stellen wir den Pilotton als klassisches 3D-Bild dar. Hier erkennt man deutlich die Harmonischen bei 2Hz, 3kHz usw.
_pilot_3D.png)
In ideales Übertragungssystem würde nur den Ton bei 1kHz zeigen. Durch Nicht-lineare Effekte werden Oberwellen erzeugt.
Zum Ausmessen verwendet man eher eine normale spektrale Darstellung (FFT)
_pilot_FFT.png)
Die erste Oberwelle bei 2kHz beträgt -48dB mit Bezug auf den Pilotton. Die Verzerrungen liegen damit um Größenordnungen unter denen von modernen digitalen Aufzeichnungssystemen. Diese erreichen Verzerrungen unterhalb von -120dB (z.B. APX555 von Audio Precision). Das sind 70dB weniger, oder als Spannungververhältnis 1:3000. Die digitalen Systeme haben damit 3000mal geringere Verzerrungen. Aber vermutlich sind es genau diese deutlichen Verzerrungen, die bei den Enthusiasten den "warmen Klang" bewirken.
An dieser Stelle möchten wir keine Diskussion pro oder contra einer LP vs. einer digitalen Aufnahme führen. Unser Ziel ist es, dass Ihr Plattenspieler die bestmöglichen Ergebnisse erzielt.
Auf der Messschallplatte ist das Testsignal so aufgenommen, dass der Pilotton auf beiden Kanälen vorhanden ist. Der Sweep ist jedoch nur auf einem Kanal. Auf dem anderen Kanal sollte daher Stille sein. Dies ist jedoch nicht der Fall, da es bedingt durch das mechanische System zu Übersprechen kommt. Diese Übersprechdämpfung sollte möglichst hoch sein.
Dieses Übersprechen erkennt man bereits aus einem einfachen Pegel-Zeitverlauf. Hier werden grob etwa 18dB erreicht.
_2ch_level_vs_time.png)
In der Auswertung wird die Übersprechdämpfung über der Frequenz aufgetragen.
_crosstalk.png)
Aus dem Sweep können auch die nicht-linearen Verzerungen (THD) über der Frequenz bestimmt werden. Wir werten 5 Oberwellen aus. Bei höheren Freuenzen z.B. 10kHz erscheint nur noch die erste Oberwelle, da weitere Oberwellen bereits im Ultraschallbereich sind. Typische Aufnahmen haben eine Abtastfrequenz von 44.1 oder 48kHz. Damit wären höhere Oberwellen bereits oberhalb der halben Abtastrate. Auf Anfrage werten wir auch Aufnahmen mit Abtastraten von 96kHz und 192kHz aus. Bitte beachten Sie, dass der Sweep auf der Testschallplatte jedoch nur bis 20kHz reicht.
_THD.png)
Die Gleichlaufschwankungen (Wow&Flutter) sind ein wichtiges Qualitätsmerkmal eines Plattenspielers. Hohe Schwankungen der Drehzahl führen zu "Leiern", geringere Schwankungen führen zu einem "rauhen" Klang. Die Grundlagen hierzu haben wir in dem verlinkten Artikel zusammengefasst.
Aus dem Pilotton der Testschallplatte kann die absolute Drehzahlabweichung und die Gleichlaufschwankungen bestimmt werden.
Schauen wir uns die Frequenz des Pilottons über der Zeit an. Eigentlich sollte dieser konstant 1000Hz betragen. Aber einen solchen "idealen" Plattenspieler gibt es nicht.
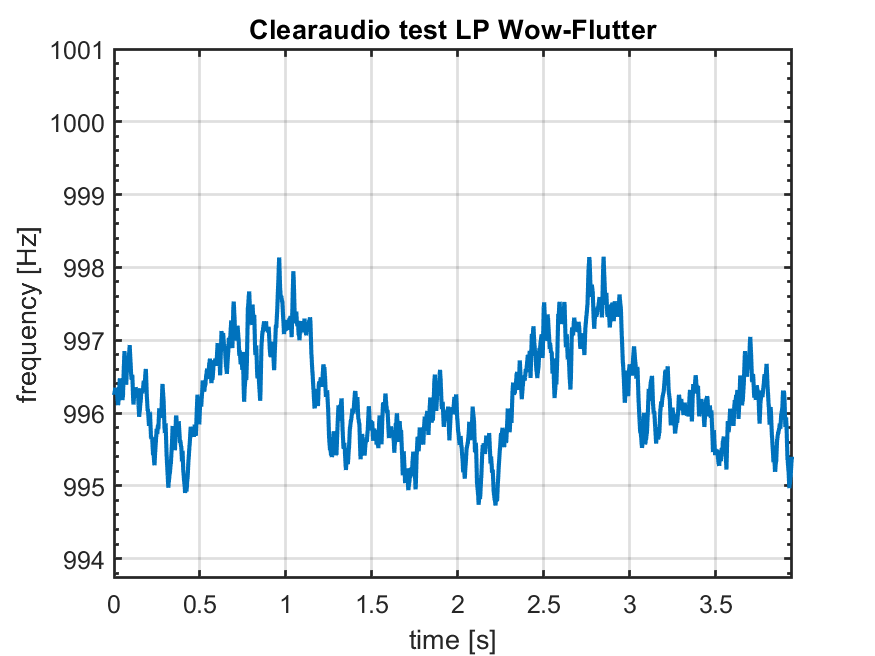
Eine andere Darstellung ist die Abweichung von der Nenndrehzahl in %.
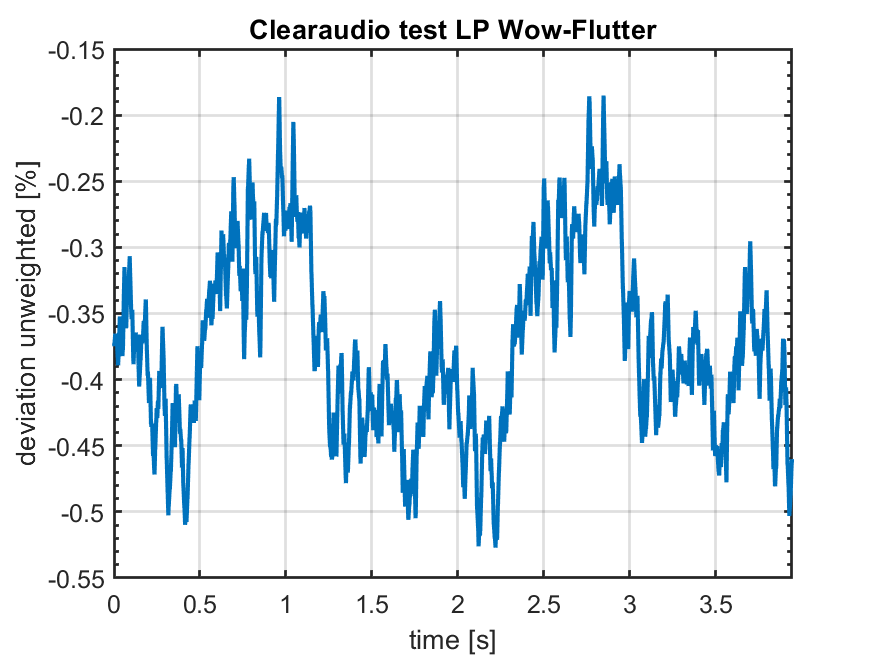
In der Audiotechnik werden diese Abweichungen in der Regel nach IEC60386 bewertet. Dieses Filter bewertet bestimmte Abweichungen stärker als andere. Die Filterkurve wurde durch umfangreich Hörtests ermittelt und international standardisiert.
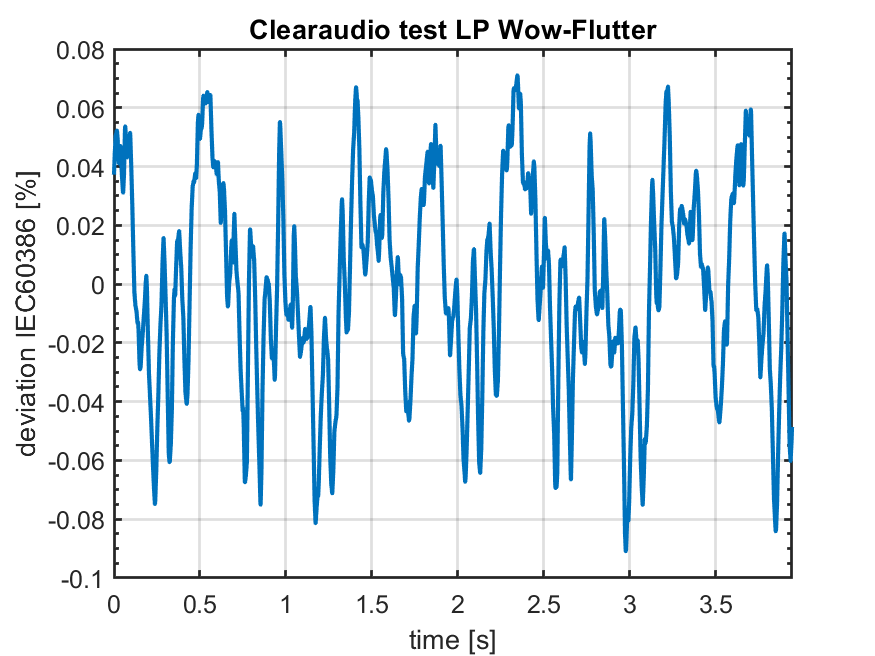
In den Datenblätter findet man nur die Mittelwerte. Die betragen für die obige Auswertung:
Abweichung von der Nenndrehzahl: -0.37%
Gleichlaufschwankungen (Wow&Flutter:
RMS unbewertet: 0.068%
RMS bewertet nach IEC60386: 0.035%
2-sigma bewertet nach IEC60386: 0.066%
Die Abweichungen sind bewertet grundsätzlich deutlich geringer. Daher muss man bei Vergleichen besonders aufpassen. In der Norm IEC60386 wird neben dem Effektivwert (RMS) der bewerteten Frequenzabweichungen ein weiterer Parameter "2-sigma" definiert. Dieser statistische Parameter gibt an, dass 95% der Momentan-Frequenzabweichungen unterhalb dieses Wertes (hier 0.066%) liegen. Es ist jetzt Zufall, dass dieser Wert ähnlich dem unbewerteten RMS liegt. Diese Werte haben nichts miteinander zu tun und müssen jeweils getrennt verglichen werden. Die einzige Gemeinsamkeit ist, dass alle drei Werte in % angegeben werden.
IEC 60386:1972/AMD1:1988
Method of measurement of speed fluctuations in sound recording and reproducing equipment
DIN IEC 60386:1995-04
Meßverfahren für Geschwindigkeitsschwankungen bei Tonaufzeichnungs- und -wiedergabegeräten (IEC 60386:1972 + A1:1988)
An dieser Stelle veröffentlichen wir Informationen und Hintergrundwissen zu Schallplattenspielern